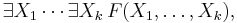Existential theory of the reals

In mathematical logic, computational complexity theory, and computer science, the existential theory of the reals is the set of all true sentences of the form

$\exists X_1 \cdots \exists X_k \, F(X_1,\dots, X_k), \,$

where F(X₁, ..., X_k) is a quantifier-free formula in the language of ordered fields with coefficients in a real closed field.^[1]

The decision problem for the existential theory of the reals is the problem of finding an algorithm that decides, for each such formula, whether it is true or false. This decision problem is NP-hard and lies in PSPACE. Thus, it has significantly lower complexity than Alfred Tarski's quantifier elimination procedure for deciding statements in the first-order theory of the reals without the restriction to existential quantifiers.^[1]

Complete problems

Several problems in computational complexity and geometric graph theory may be classified as complete for the existential theory of the reals. These include:

recognition of intersection graphs of line segments in the plane (that is, given an undirected graph, determining whether there is a set of line segments that has an isomorphic intersection graph);
recognition of unit disk graphs (again, given only the graph itself as input);
recognition of intersection graphs of convex sets in the plane;
stretchability of pseudolines (that is, given a family of curves in the plane, determining whether they are homeomorphic to a line arrangement);
determining the rectilinear crossing number of a graph (the minimum number of pairs of edges that cross in any drawing with edges drawn as straight line segments in the plane);
the algorithmic Steinitz problem (given a lattice, determine whether it is the face lattice of a convex polytope); and
testing whether a given graph can be drawn in the plane with a given set of edge pairs as its crossings.\
testing whether a 4-regular graph whose edges are colored with four colors has a drawing with edges as straight line segments of four slopes, with the slopes representing the colors in the coloring.^[2]

Based on this, the complexity class $\exists \mathbb{R}$ has been defined as the set of problems having a polynomial-time reduction to the existential theory of the reals.^[3]

References

^ ^a ^b Basu, Saugata; Pollack, Richard; Roy, Marie-Françoise (2006), "Existential Theory of the Reals", Algorithms in Real Algebraic Geometry, Algorithms and Computation in Mathematics, 10 (2nd ed.), Springer-Verlag, pp. 505–532, doi:10.1007/3-540-33099-2_14, ISBN 9783540330981 .
^ Richter, David A. (2011), "How to draw a Tait-colorable graph", in Brandes, Ulrik; Cornelsen, Sabine, Proc. 18th International Symposium on Graph Drawing (GD 2010), Lecture Notes in Computer Science, 6502, Springer-Verlag, pp. 353–364, doi:10.1007/978-3-642-18469-7_32 .
^ Schaefer, Marcus (2010), "Complexity of some geometric and topological problems", Graph Drawing, 17th International Symposium, GS 2009, Chicago, IL, USA, September 2009, Revised Papers, Lecture Notes in Computer Science, 5849, Springer-Verlag, pp. 334–344, doi:10.1007/978-3-642-11805-0_32, http://ovid.cs.depaul.edu/documents/convex.pdf .